基于稀疏傅里葉變換的氯氣流量計流量分析
點擊次數:1916 發布時間:2021-01-08 06:39:43
摘要:傳統的渦街信號處理方法主要是用傅里葉變換,由于傳統的傅里葉變換的時間復雜度與其分析的信號長度成正比,采樣點數越多其頻譜譜線越接近理想狀態,但需要較大的運算時間。 針對這個問題,提出了采用稀疏傅里葉變換分析渦街流量信號的方法,利用實驗數據進行 Matlab 仿真,驗證了該方法的性能優于傳統的方法,不僅提高了對強噪聲的抗干擾能力還加快了計算速度。
近半個世紀以來, 氯氣流量計因其測量精度高、 無可動部件、測量精度高等優點得到了迅猛的發展。 氯氣流量計主要測量部件為壓電傳感器,其易受到噪聲的干擾,如管道振動、電磁干擾、流體的低頻擺動等。 在含有噪聲的信號的中提取出有用的渦街信號, 國內外眾多研究學者對渦街信號的處理方式主要有FFT 的周期圖法、互相關法、自適應陷波濾波法、小波分析法和數字跟蹤濾波方法等 。 但是這些方法對于含有強噪聲的信號測量精度不高或錯誤,即噪聲頻率在渦街信號頻率范圍內,而噪聲的幅值高于渦街信號的幅值。 本文提出一種基于稀疏傅里葉變換的渦街信號分析方法, 該方法不僅具有很高的實時性而且對含有強噪聲的信號也能夠保證測量的準確性。
1 稀疏傅里葉變換的理論分析
快速傅里葉變換( Fast Fourier Transform , FFT )的時間復雜度為 O ( nlogn ),與離散傅里葉變換( Discrete Fourier Trans-form , DFT )的復雜度 O ( N 2 )相比,運算速度發生了質的飛躍,尤其是隨著采樣點數 N 的增加這種優勢就越加明顯 。但是隨著時代的發展,需要實時處理的信號越來越多,即便是 FFT 對于這樣的需求也難以滿足。 傳統的 FFT 只考慮到了信號的長度 N 需要為 2 的整數次冪,并未考慮到信號的自身的特性,如稀疏性。
在實際生活中常見的信號的傅里葉系數只有小部分是我們感興趣的,其大部分都是可以忽略的,如圖像和語音信號 。 針對這樣的信號能否找到一種更加快速的算法來計算其傅里葉變換,MIT的團隊給出了答案 。 該團隊提出了稀疏傅里葉變換( Sparse Fourier Transform , SFT ), 該算法利用了信號頻域的稀疏性,先對信號進行分“桶”,將長的 DFT 運算變為較短的運算,再根據一定的規則重構了信號的頻譜,其運算速度為 FFT 的十倍甚至百倍 。
稀疏傅里葉變換使用的先決條件就是分析的信號具有稀疏性,設 x ( n )是長度為 N 點的有限長序列,則該序列的 N 點離散傅里葉變換逆變換為:
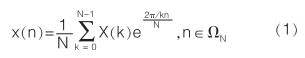
其中 Ω N 表示集合 邀0 , 1 ,……, N-1妖 。 只有 K ( K塏N )個非零的傅里葉系數,只通過信號 x ( n )的部分采樣值來確定這 K 非零傅里葉系數與位置。
1.1 頻域降采樣
參數 B 整除 N ,若想要以等間隔 N/B 對信號頻域進行降采樣,即:

混疊后頻域譜線由 N 減少到 B ,信號點數成倍較少,這正是SFT 算法復雜度為亞線性的關鍵原因之一。
1.2 稀疏傅里葉變換運算步驟
稀疏傅里葉變換包括頻譜重排、加窗函數、頻域降采樣、定位、估值與迭代等運算過程。
1.2.1 頻譜重排
頻譜重排的目的是使各大值點均勻分布, 分桶時大頻點不要分到同一個桶中,當兩個或兩個以上大值點在同一桶中時,無法求解取大值點的頻率和位置。p ( n ) =x { mod [ σ · n , N ]}, nε [ 1 , N ] ( 4 )式中 σ 為一個隨機數,且為奇數,并滿足 mod [ σ×σ -1 , N ] =1 ,這就保證了 σ 與 N 互為質數, σ -1 為 σ 的模逆算子。 根據傅里葉變換可知上式中的 p ( n ), x ( n )滿足:P ( k ) =X { mod [ σ-1 · k , N ]}, σ , kε [ 1 , N ] ( 5 )通過式( 4 )、( 5 )知道信號時域上的重排也會導致頻譜信號位置上發生變換。
1.2.2 窗函數濾波器
為了保證算法的效率且防止頻譜泄漏,需要設計一個在時域和頻域能量都集中的濾波器, 根據文獻該濾波器的為 sinc 窗函數與高斯窗函數的卷積,該窗函數具有過渡帶陡峭、通帶平滑等特點。
1.2.3 哈希映射
定義一個映射區間 Ω N →Ω B 的哈希函數: h σ ( k ) =round ( σ ·k · N/B ), round 表示四舍五入, 將 Ω N 中每一個點都映射到 Ω B中。 定義偏移量: o σ ( k ) =σ · k-h σ ( k )·( N/B );定義集合 J ,集合 J包含了 Z ( k 中 K 個較大幅值的坐標 k ;通過哈希反映射得到 I r ,即 I r =邀kε [ 0 , N-1 ] |h σ ( k ) εJ妖 ,*后從中取出 K 個大值點對原信號的頻率估計。
1.2.4 循環投票
對于每一個 kεI , X‘( k ) =Z ( h σ ( k ) W Nτk/G ( o σ ( k ))頻率估計值。 每一次定位循環得到一個坐標集合 I r ,在 L=O ( log 2 N )次循環中,對任意坐標 kεI=I 1 U …… υI r ,若出現次數大于 L/2 ,則將其歸入集合 I‘ 中,并認為集合 I‘ 包含所有目標頻點坐標。 對每一個kεI‘ ,取 L 次循環得到 X ( k )的中值作為*終的頻率值,即:X ( k ) =median ( 邀X r ( k ) |rε邀1 ,……, L)
2 渦街信號的特點
在一定范圍內,流體流速 V 與渦街頻率 f 有以下關系:
f=πK 1 VD2/4 ( 6 )
其中 K 1 為儀表系數, D 為管道直徑。在管道口徑 D 不變,流體密度不變的情況下,渦街傳感器的輸出幅值與 f 2 成正比,具體表達形式可以根據實驗測出。本文以 50mm 口徑氣體實驗為例,數據如表 1 所示:

從表 1 的氣體流量的實際幅值和擬合幅值的誤差可以看出,渦街信號的幅值在理論值附近波動,且波動的范圍一定,則幅頻關系更一般的形式表達如下:
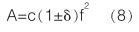
其中 c 為系數, δ 為相對誤差限, 其示意圖如圖 2 所示,圖中實線為幅頻關系的理論擬合曲線, 而虛線為幅值波動的閾值曲線。根據實驗的數據,渦街信號幅值波動的相對誤差為 ±10% 。

3 實驗仿真
本實驗采用基于對管道振動信號進行分析, 其采樣點數為2048 ,采用稀疏傅里葉變換對數據進行頻譜分析。 如圖 3 所示。
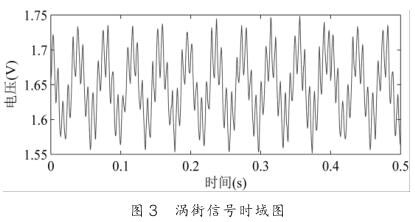
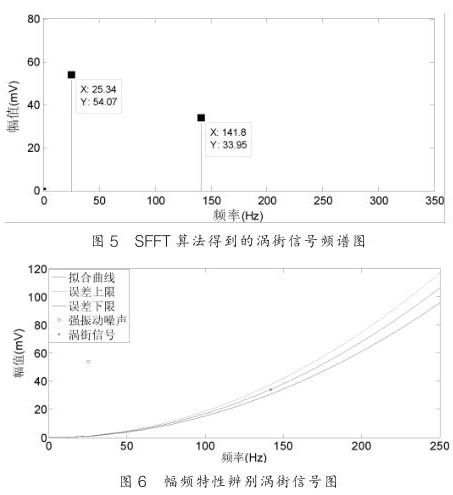
圖 4 是用 FFT 算法對渦街時域信號分析后得到的頻譜圖,其中渦街信號頻率為 141.8Hz ,振動噪聲信號頻率為 25.34Hz 。從圖中可以看出,信號是稀疏的,稀疏度 K=2 。
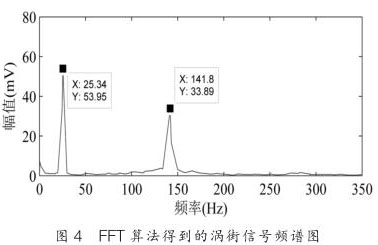
從圖 5 可以看出 SFT 算法能夠很好恢復,對渦街信號的頻率恢復沒有誤差,而幅值的誤差不超過 1% ,這對含有強振動噪聲的渦街信號精確測量至關重要;圖 6 是經 SFT 頻譜分析所得到的數據通過幅頻特性曲線來辨別是噪聲信號還是渦街信號。通過幅頻關系的信號處理方法可以從含有振動的混合信號中識別渦街信號,從而達到提高氯氣流量計抗振動性能的目的。
現在分析 SFT 算法的優越性。 基于哈希映射的稀疏傅里葉變換算法的時間復雜度為
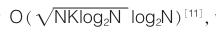
由前文可知 FFT 算法時間復雜度為 O ( Nlog 2 N )。 隨著信號長度 N 的增長,兩者的時間復雜度也會發生變化。 采用時間復雜度的數量級的比值來刻畫這種變化:
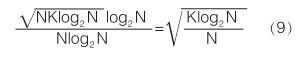
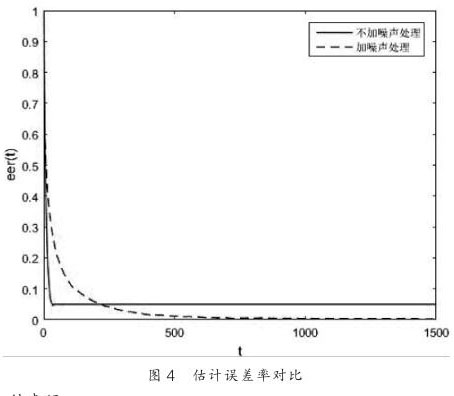
當 K=2 ,SFT 算法與 FFT 算法的時間復雜度的比值關系如圖 7 所示。處理的 ROBLOCAM-CN 算法進行對比,其估計誤差率 eer(t)對比效果如圖 4 所示。從對比結果中可以看到,若不對通信噪聲進行處理則各自由節點和墻的位置始終存在偏差 , 而 在ROBLOCAM-CN 算法下所有的自由節點與墻都迅速收斂至各自的精確位置,驗證了本算法的有效性和魯棒性。 各節點的收斂軌跡和*終的定位與環境構建效果如圖 5 所示。
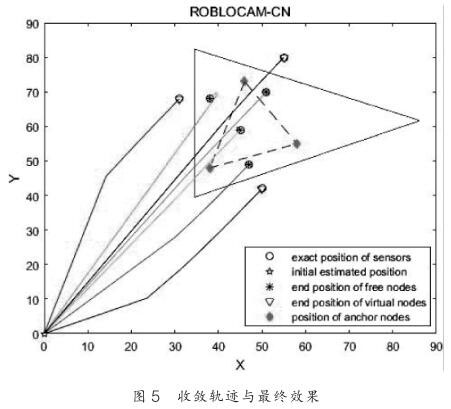
5 結束語
本文提出了一種噪聲情形下新穎的室內定位與環境構建算法,該算法不需要無線傳感器網絡中的節點配備激光傳感模塊,只需要通過節點間的射頻信號即可實現對周圍環境的感知,為室內定位與環境構建技術提供了一種經濟且可靠的解決方案。
耐腐型測氯氣流量計對于防腐制造工藝的研究探討
運用等離子清清洗方式清除氯氣流量計葉片表面附著物
基于稀疏傅里葉變換的氯氣流量計流量分析
氯氣流量計加氣站BOG產生的原因和控制方法
關于氯氣流量計在汽輪機改造中的應用及安裝調試
氯氣流量計的電磁干擾路徑與電磁兼容特性分析
關于氯氣流量計在工業生產及貿易結算中的選型設計
氯氣流量表,氯氣流量用什么流量計測量
氯氣流量計廠家
氯氣流量計價格
氯氣流量計選型
氯氣專用流量計,氯氣流量表價格
氯氣流量表,氯氣流量選用什么流量計
氯氣專用流量計
氯氣流量用什么流量計測量
氯氣流量計選型遇到的常見故障怎么調怎么排除
氯氣流量計產品特點及使用規范
氯氣流量選用什么流量計
氯氣流量表,氯氣專用流量計
解決氯氣流量計故障的實驗方案說明
近半個世紀以來, 氯氣流量計因其測量精度高、 無可動部件、測量精度高等優點得到了迅猛的發展。 氯氣流量計主要測量部件為壓電傳感器,其易受到噪聲的干擾,如管道振動、電磁干擾、流體的低頻擺動等。 在含有噪聲的信號的中提取出有用的渦街信號, 國內外眾多研究學者對渦街信號的處理方式主要有FFT 的周期圖法、互相關法、自適應陷波濾波法、小波分析法和數字跟蹤濾波方法等 。 但是這些方法對于含有強噪聲的信號測量精度不高或錯誤,即噪聲頻率在渦街信號頻率范圍內,而噪聲的幅值高于渦街信號的幅值。 本文提出一種基于稀疏傅里葉變換的渦街信號分析方法, 該方法不僅具有很高的實時性而且對含有強噪聲的信號也能夠保證測量的準確性。
1 稀疏傅里葉變換的理論分析
快速傅里葉變換( Fast Fourier Transform , FFT )的時間復雜度為 O ( nlogn ),與離散傅里葉變換( Discrete Fourier Trans-form , DFT )的復雜度 O ( N 2 )相比,運算速度發生了質的飛躍,尤其是隨著采樣點數 N 的增加這種優勢就越加明顯 。但是隨著時代的發展,需要實時處理的信號越來越多,即便是 FFT 對于這樣的需求也難以滿足。 傳統的 FFT 只考慮到了信號的長度 N 需要為 2 的整數次冪,并未考慮到信號的自身的特性,如稀疏性。
在實際生活中常見的信號的傅里葉系數只有小部分是我們感興趣的,其大部分都是可以忽略的,如圖像和語音信號 。 針對這樣的信號能否找到一種更加快速的算法來計算其傅里葉變換,MIT的團隊給出了答案 。 該團隊提出了稀疏傅里葉變換( Sparse Fourier Transform , SFT ), 該算法利用了信號頻域的稀疏性,先對信號進行分“桶”,將長的 DFT 運算變為較短的運算,再根據一定的規則重構了信號的頻譜,其運算速度為 FFT 的十倍甚至百倍 。
稀疏傅里葉變換使用的先決條件就是分析的信號具有稀疏性,設 x ( n )是長度為 N 點的有限長序列,則該序列的 N 點離散傅里葉變換逆變換為:
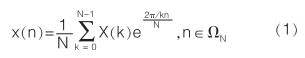
其中 Ω N 表示集合 邀0 , 1 ,……, N-1妖 。 只有 K ( K塏N )個非零的傅里葉系數,只通過信號 x ( n )的部分采樣值來確定這 K 非零傅里葉系數與位置。
1.1 頻域降采樣
參數 B 整除 N ,若想要以等間隔 N/B 對信號頻域進行降采樣,即:

混疊后頻域譜線由 N 減少到 B ,信號點數成倍較少,這正是SFT 算法復雜度為亞線性的關鍵原因之一。
1.2 稀疏傅里葉變換運算步驟
稀疏傅里葉變換包括頻譜重排、加窗函數、頻域降采樣、定位、估值與迭代等運算過程。
1.2.1 頻譜重排
頻譜重排的目的是使各大值點均勻分布, 分桶時大頻點不要分到同一個桶中,當兩個或兩個以上大值點在同一桶中時,無法求解取大值點的頻率和位置。p ( n ) =x { mod [ σ · n , N ]}, nε [ 1 , N ] ( 4 )式中 σ 為一個隨機數,且為奇數,并滿足 mod [ σ×σ -1 , N ] =1 ,這就保證了 σ 與 N 互為質數, σ -1 為 σ 的模逆算子。 根據傅里葉變換可知上式中的 p ( n ), x ( n )滿足:P ( k ) =X { mod [ σ-1 · k , N ]}, σ , kε [ 1 , N ] ( 5 )通過式( 4 )、( 5 )知道信號時域上的重排也會導致頻譜信號位置上發生變換。
1.2.2 窗函數濾波器
為了保證算法的效率且防止頻譜泄漏,需要設計一個在時域和頻域能量都集中的濾波器, 根據文獻該濾波器的為 sinc 窗函數與高斯窗函數的卷積,該窗函數具有過渡帶陡峭、通帶平滑等特點。
1.2.3 哈希映射
定義一個映射區間 Ω N →Ω B 的哈希函數: h σ ( k ) =round ( σ ·k · N/B ), round 表示四舍五入, 將 Ω N 中每一個點都映射到 Ω B中。 定義偏移量: o σ ( k ) =σ · k-h σ ( k )·( N/B );定義集合 J ,集合 J包含了 Z ( k 中 K 個較大幅值的坐標 k ;通過哈希反映射得到 I r ,即 I r =邀kε [ 0 , N-1 ] |h σ ( k ) εJ妖 ,*后從中取出 K 個大值點對原信號的頻率估計。
1.2.4 循環投票
對于每一個 kεI , X‘( k ) =Z ( h σ ( k ) W Nτk/G ( o σ ( k ))頻率估計值。 每一次定位循環得到一個坐標集合 I r ,在 L=O ( log 2 N )次循環中,對任意坐標 kεI=I 1 U …… υI r ,若出現次數大于 L/2 ,則將其歸入集合 I‘ 中,并認為集合 I‘ 包含所有目標頻點坐標。 對每一個kεI‘ ,取 L 次循環得到 X ( k )的中值作為*終的頻率值,即:X ( k ) =median ( 邀X r ( k ) |rε邀1 ,……, L)
2 渦街信號的特點
在一定范圍內,流體流速 V 與渦街頻率 f 有以下關系:
f=πK 1 VD2/4 ( 6 )
其中 K 1 為儀表系數, D 為管道直徑。在管道口徑 D 不變,流體密度不變的情況下,渦街傳感器的輸出幅值與 f 2 成正比,具體表達形式可以根據實驗測出。本文以 50mm 口徑氣體實驗為例,數據如表 1 所示:

從表 1 的氣體流量的實際幅值和擬合幅值的誤差可以看出,渦街信號的幅值在理論值附近波動,且波動的范圍一定,則幅頻關系更一般的形式表達如下:
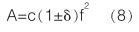
其中 c 為系數, δ 為相對誤差限, 其示意圖如圖 2 所示,圖中實線為幅頻關系的理論擬合曲線, 而虛線為幅值波動的閾值曲線。根據實驗的數據,渦街信號幅值波動的相對誤差為 ±10% 。

3 實驗仿真
本實驗采用基于對管道振動信號進行分析, 其采樣點數為2048 ,采用稀疏傅里葉變換對數據進行頻譜分析。 如圖 3 所示。

圖 4 是用 FFT 算法對渦街時域信號分析后得到的頻譜圖,其中渦街信號頻率為 141.8Hz ,振動噪聲信號頻率為 25.34Hz 。從圖中可以看出,信號是稀疏的,稀疏度 K=2 。

從圖 5 可以看出 SFT 算法能夠很好恢復,對渦街信號的頻率恢復沒有誤差,而幅值的誤差不超過 1% ,這對含有強振動噪聲的渦街信號精確測量至關重要;圖 6 是經 SFT 頻譜分析所得到的數據通過幅頻特性曲線來辨別是噪聲信號還是渦街信號。通過幅頻關系的信號處理方法可以從含有振動的混合信號中識別渦街信號,從而達到提高氯氣流量計抗振動性能的目的。

現在分析 SFT 算法的優越性。 基于哈希映射的稀疏傅里葉變換算法的時間復雜度為
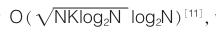
由前文可知 FFT 算法時間復雜度為 O ( Nlog 2 N )。 隨著信號長度 N 的增長,兩者的時間復雜度也會發生變化。 采用時間復雜度的數量級的比值來刻畫這種變化:
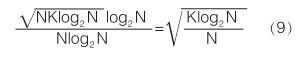
當 K=2 ,SFT 算法與 FFT 算法的時間復雜度的比值關系如圖 7 所示。處理的 ROBLOCAM-CN 算法進行對比,其估計誤差率 eer(t)對比效果如圖 4 所示。從對比結果中可以看到,若不對通信噪聲進行處理則各自由節點和墻的位置始終存在偏差 , 而 在ROBLOCAM-CN 算法下所有的自由節點與墻都迅速收斂至各自的精確位置,驗證了本算法的有效性和魯棒性。 各節點的收斂軌跡和*終的定位與環境構建效果如圖 5 所示。


5 結束語
本文提出了一種噪聲情形下新穎的室內定位與環境構建算法,該算法不需要無線傳感器網絡中的節點配備激光傳感模塊,只需要通過節點間的射頻信號即可實現對周圍環境的感知,為室內定位與環境構建技術提供了一種經濟且可靠的解決方案。



